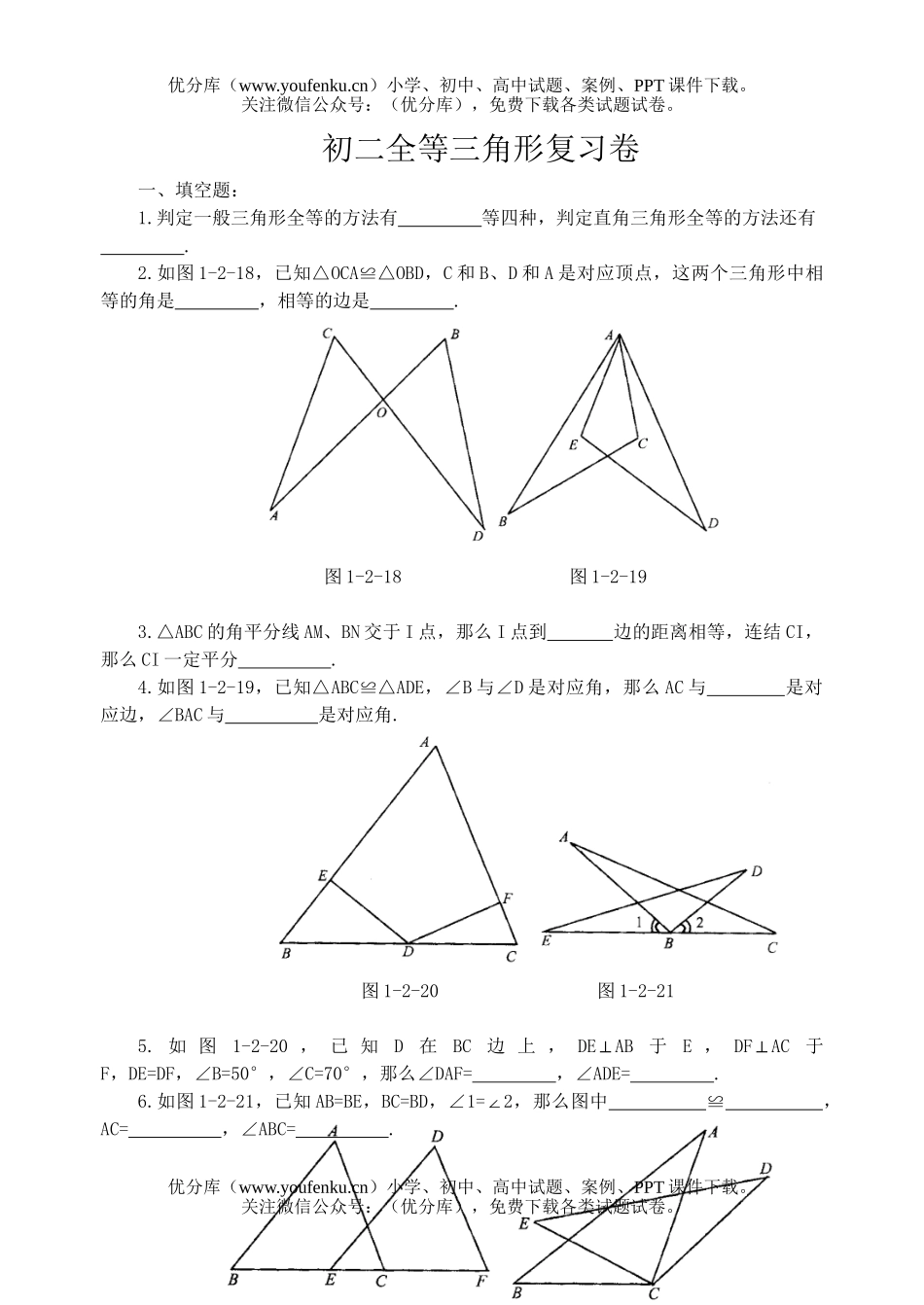
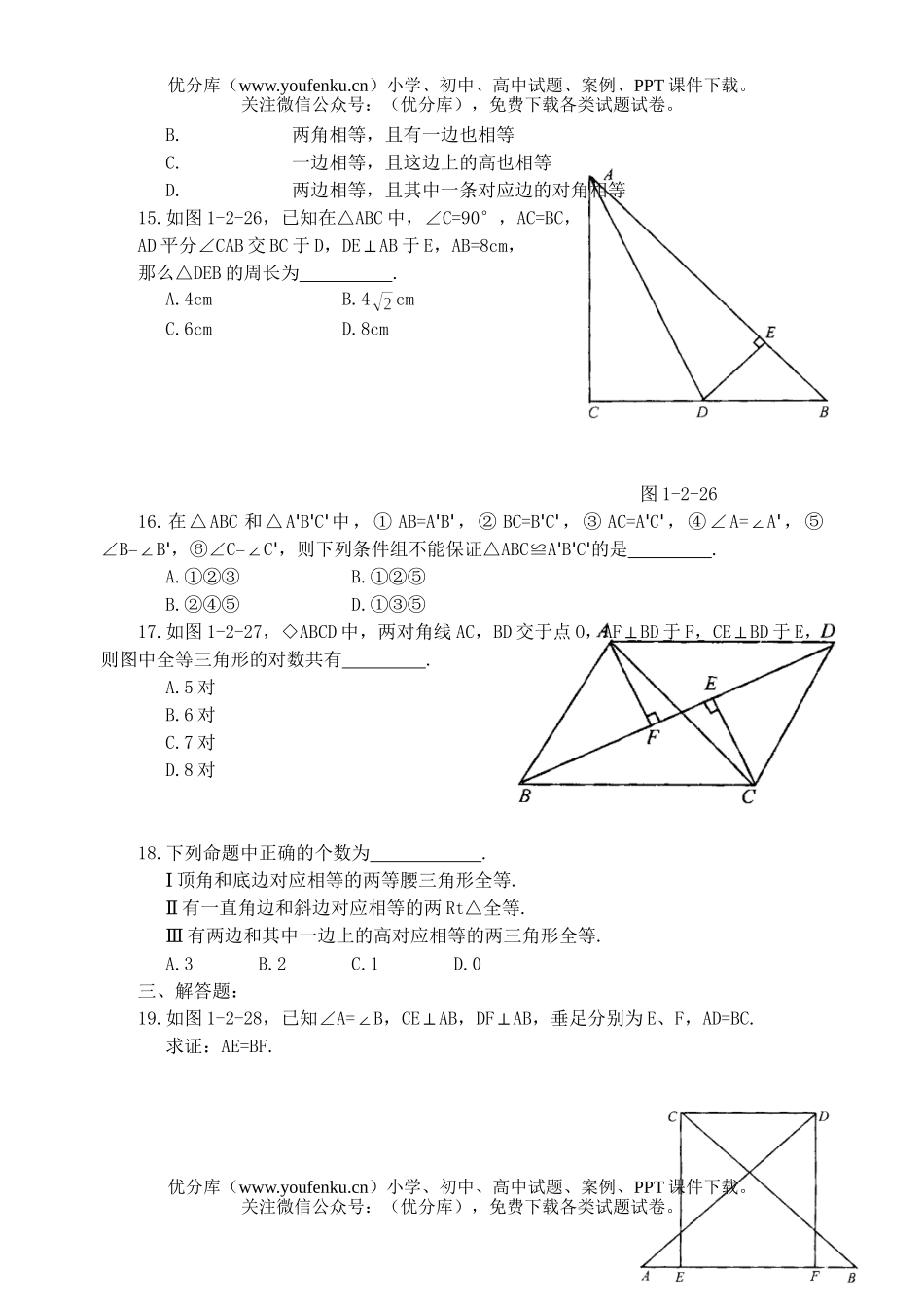
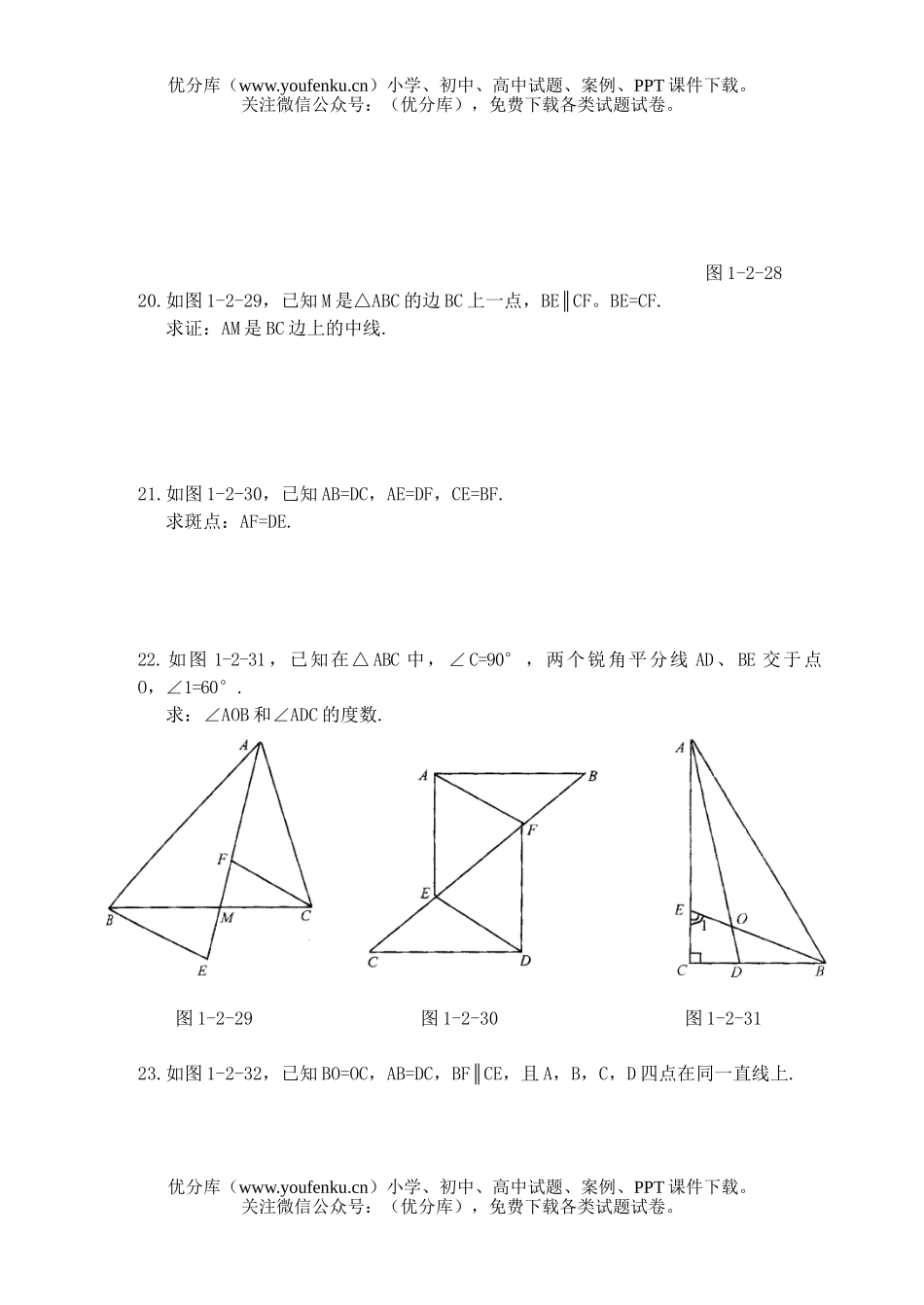
本次试卷是初二数学的全等三角形复习卷,旨在巩固学生对于全等三角形概念的理解和应用能力。通过这份试卷,我们希望学生能够熟练掌握全等三角形的判定条件、性质和应用技巧,进一步提升他们的数学思维和解题能力。
试卷的背景信息:
在设计这份试卷时,我们深入研究了初二数学教材中有关全等三角形的章节内容,结合学生的学习状况和能力水平,充分考虑了他们在全等三角形知识上的掌握程度和易错点。同时,我们还参考了教学大纲和其他教学资源,以确保试卷的设计符合课程要求和学生学习的整体目标。
试卷的内容:
本试卷分为五个部分:选择题、填空题、判断题、计算题和应用题。下面将详细解读试卷中的每一个部分,包括试题的要求、所需的知识点及解答方法。
1.选择题部分:
这一部分共有20个题目,每题有四个选项。学生需要仔细阅读题目,根据所学的全等三角形知识,选出正确答案。这些题目涵盖了全等三角形判定条件、全等三角形的性质和等式的证明等方面。
举例:
下列哪个条件不能用来判定两个三角形全等?
A. SSS
B. SAS
C. AAA
D. ASA
2.填空题部分:
本部分共有10道题目,需要学生根据题目要求,填写正确的答案或解释。题目的难度逐渐增加,考察学生对全等三角形性质和推理的理解和应用能力。
举例:
两个全等的三角形,其对应角度相等、对应边长相等。这个命题是全等三角形的(填入一个词)。
3.判断题部分:
该部分包含10道判断题,学生需要判断给定的陈述是否正确。这些题目涉及到全等三角形的性质、判定条件以及应用技巧。
举例:
如果两个对角相等的四边形ABC和DCBA,那么它们一定是全等的。
4.计算题部分:
本部分共有5道题目,要求学生进行具体的计算和推理,包括计算全等三角形的边长和角度。
举例:
在三角形ABC和三角形DEF中,已知∠A=∠D=36°,∠B=∠E=64°,而BC=12cm。如果AC与EF全等,求EF的长度。
5.应用题部分:
最后一部分是应用题,设计了一些实际问题,要求学生运用全等三角形的知识解决实际问题。这些题目旨在培养学生的应用能力和解决问题的思维。
举例:
甲乙两地相距800千米,为了测量两地之间的距离,科学家利用了全等三角形原理进行测量。已知科学家在甲地A处测量得到∠BAC=60°,在乙地B处测量得到∠ABC=45°,请计算出两地之间的距离。
试卷的目标受众:
该试卷主要面向初二学生。通过这份试卷,学生可以进一步巩固和拓展对全等三角形的理解和应用能力,为他们在数学学习中打下坚实的基础。此外,通过解答试卷中的各种题型,学生还可以培养数学推理和解决实际问题的能力,提高他们的数学思维水平。
在整篇文章中,我们充分运用了与试卷相关的关键词,同时保持文章的流畅性和一致性。这样不仅可以提升文章在搜索引擎的相关性评分,还能为读者提供有价值的信息。